
( 2017).ĭue to the randomness in the updates, the sequence of iterates of a stochastic optimisation algorithm forms a stochastic process rather than a deterministic sequence.

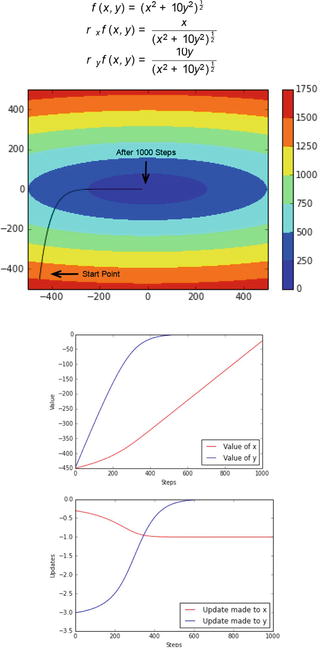
This is highly relevant for target functions in, e.g., deep learning, since those are often non-convex see Choromanska et al. Aside from a higher efficiency, this randomness can have a second effect: The perturbation introduced by subsampling can allow to escape local extrema and saddle points. In subsampling the aforementioned small fraction of the data set is picked randomly in every iteration. The stochasticity of the algorithms is typically induced by subsampling. Stochastic optimisation algorithms that only consider a small fraction of the data set in each step have shown to cope well with this issue in practice see, e.g., Bottou ( 2012), Chambolle et al. This leads to an immense computational cost.
#Stochastic gradient descent full
Those methods require evaluations of the loss function with respect to the full big data set in each iteration. Classical algorithms being gradient descent or the (Gauss–)Newton method see Nocedal and Wright ( 2006). Solving this problem with classical optimsation algorithms is usually infeasible. The training is usually phrased as an optimisation problem. The training of models with big data sets is a crucial task in modern machine learning and artificial intelligence. We conclude after a discussion of discretisation strategies for the stochastic gradient process and numerical experiments. In this case, the process converges weakly to the point mass concentrated in the global minimum of the full target function indicating consistency of the method.
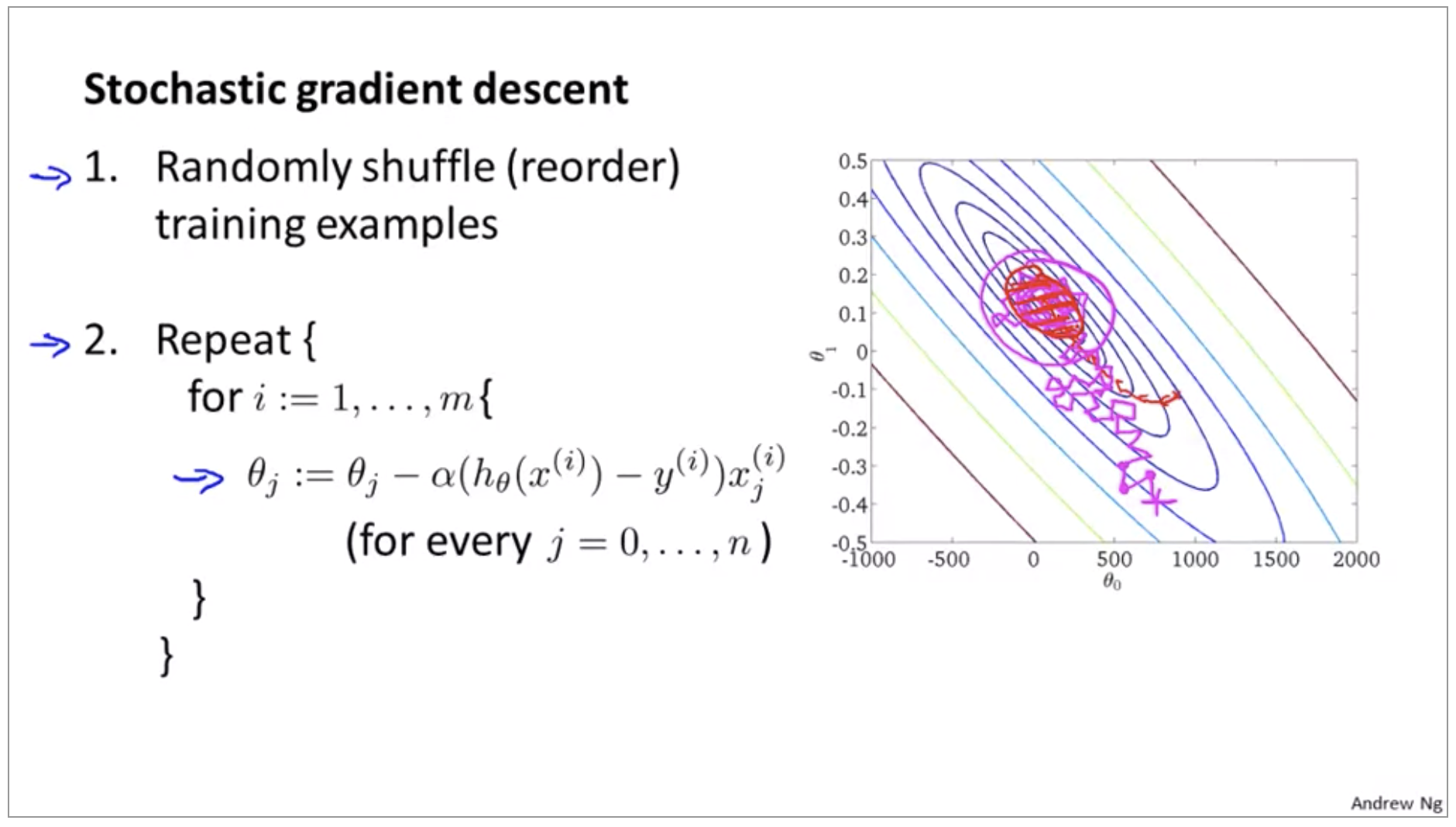
Then we study the case, where the learning rate goes to zero sufficiently slowly and the single target functions are strongly convex. We give conditions under which the stochastic gradient process with constant learning rate is exponentially ergodic in the Wasserstein sense. After introducing it, we study theoretical properties of the stochastic gradient process: We show that it converges weakly to the gradient flow with respect to the full target function, as the learning rate approaches zero. Processes of this type are, for instance, used to model clonal populations in fluctuating environments. The dynamical system-a gradient flow-represents the gradient descent part, the process on the finite state space represents the random subsampling. The stochastic gradient process is a dynamical system that is coupled with a continuous-time Markov process living on a finite state space. In this work, we introduce the stochastic gradient process as a continuous-time representation of stochastic gradient descent. With large data sets with millions of examples, and after a reasonable amount of iterations, the value of the cost function will be extremely close to the minimum that any differences will be negligible.Stochastic gradient descent is an optimisation method that combines classical gradient descent with random subsampling within the target functional. Stochastic gradient descent does not always converge to the minimum of the cost function, instead, it will continuously circulate the minimum. Over time, the general direction of the stochastic gradient descent will converge to close to the minimum. However in stochastic gradient descent, as one example is processed per iteration, thus there is no guarantee that the cost function reduces with every step. This takes less computational power compared to the batch gradient descent, which iterates through all the examples in a data set before aiming to reduce the cost function. Unlike batch gradient descent, which is computationally expensive to run on large data sets, stochastic gradient descent is able to take smaller steps to be more efficient while achieving the same result.Īfter randomization of the data set, stochastic gradient descent performs gradient descent based on one example, and start to change the cost function.
#Stochastic gradient descent series
Similar to batch gradient descent, stochastic gradient descent performs a series of steps to minimize a cost function. Stochastic gradient descent is an optimization algorithm which improves the efficiency of the gradient descent algorithm.


 0 kommentar(er)
0 kommentar(er)
